Ferraillage d’une plaque BA et calcul aux éléments finis

1. OBJET DE LA NOTE

Dans le cadre du projet de la Maison de l’Ordre des Avocats sur la ZAC des Batignolles à Paris, nous avons été amenés à utiliser, conjointement avec le CTICM en charge des études d’exécution de la charpente métallique, le logiciel de modélisation aux éléments finis SCIA.

Lors de l’exploitation des résultats nous nous sommes interrogés, avec la Maîtrise d’œuvre, sur la manière de les interpréter pour définir le ferraillage. La détermination de l’armature s’est posée en particulier pour le radier pontant la ligne n°13 de métro compte tenu de sa géométrie triangulaire atypique.

Afin de fiabiliser l’exploitation des résultats nous avons comparé les résultats obtenus, sur un modèle test avec 3 logiciels MEF à savoir ROBOT STRUCTURAL ANALYSIS PROFESSIONAL de chez AUTODESK, ADVANCE DESIGN de chez GRAITEC et SCIA ENGINEER de chez SCIA.

Dans cette note nous faisons un rappel synthétique des différentes méthodes utilisées dans les calculs automatiques aux éléments finis. Puis nous présentons les résultats issus des différents modèles test.

2. RAPPELS DES DIFFÉRENTES MÉTHODES UTILISÉES

Il existe plusieurs méthodes pour déterminer le ferraillage, nous étudions ci-dessous les deux méthodes le plus couramment utilisées par les logiciels MEF : la méthode de Wood, la méthode Capra-Maury, et la méthode de Baumann.

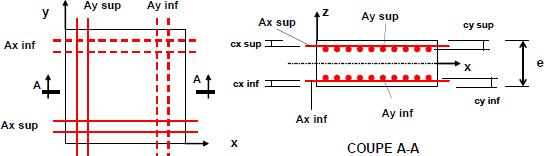
a. Convention

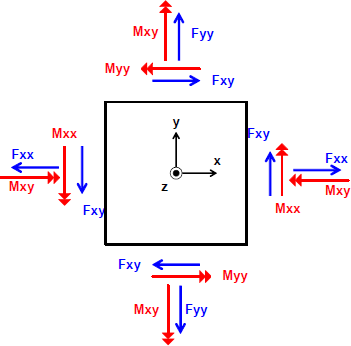On considère un élément infiniment petit => pas de variation des efforts. Efforts de membrane :             Fxx, Fyy et Fxy (en T/ml)

Moments (flexion, torsion) :     Mxx, Myy et Mxy (en T.m/ml) Selon le théorème de Cauchy, les cisaillements sont identiques sur les différentes faces

Conventions de signes :

• F > 0 en traction
• M > 0 s’il tend la face sup (z>0)
• Mxy > 0 s’il crée des cisaillements > 0 en face supérieure.

 

b. Méthode Wood

Effort sollicitant sur une facette

Pour illustrer la méthode, nous étudions une plaque soumise uniquement à de la flexion.

 

 

 

 

 

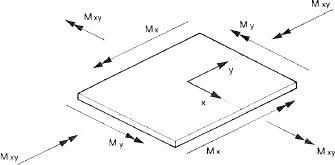
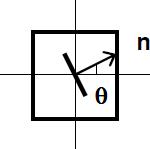
Les efforts s’exerçant sur une facette quelconque d’angle q selon la théorie des plaques sont :

M x’ = Mx cos ² (q) + My sin ² (q) + 2 Mxy sin (q) cos (q)

M xy’ = ( My – Mx )* sin (q) cos (q) + Mxy * cos(2q) Et sur la facette perpendiculaire à cette facette:

M y’ = Mx cos ² (q +p/2) + My sin ² (q +p/2) + 2 Mxy sin(q +p/2) cos(q +p/2)

M xy’ = ( My – Mx )* sin (q) cos (q) + Mxy * cos(2 q)

 

Ci-dessous la démonstration détaillée issue d’un extrait d’un document

d’ENPC (https://educnet.enpc.fr/mod/resource/view.php?id=7112) :

Effort résistant sur une facette

Pour une direction α de l’armature donnée R(α), la projection du moment résistant sur l’axe n selon le

critère de Johansen est :

R(q)= R(α) cos (q -α)²

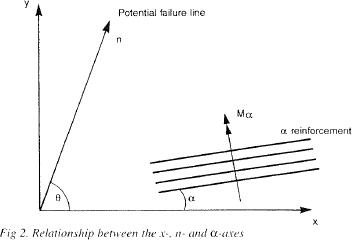
Pour le cas classique d’un réseau orthogonal d’armatures Ax, Ay (cm2/ml), nous avons :

En appliquant les relations de changement de base, on aura dans un repère tourné d’un angle q : R(q) = C².Rx + S².Ry

Pour des aciers de direction quelconque, nous avons : R(q) = C².Rx + S².Ry + 2CS Rxy

Avec

Rx = Σ R(α) C² Ry = Σ R(α) S²

Rxy = Σ R(α) CS (= 0 si 2 direction orthogonale de ferraillage)

Mise en équation

La résistance de la section sera assurée si R(q) > M(q) si quel que soit la facette : C².Rx + S².Ry > C². Mx + S².My + 2CS.Mxy quel que soit l’angle q                      (1) Pour q = 0 :                   C = 1 et S = 0 =>           Rx > Fxx

Pour q = p /2 :              C = 0 et S = 1 =>           Ry > Fyy

Si on prend juste Rx = Mxx et Ry = Myy, la relation (1) ci-dessus ne sera pas vérifiée pour certains angles

q, à cause de la torsion Mxy.

Pour détermination les sections d’acier à mettre en plus du Mxx et Myy On pose Dx = Rx – Mxx et Dy = Ry – Myy

L’équation (1) devient :             C² . Dx + S² . Dy > 2CS . Mxy                  (2)

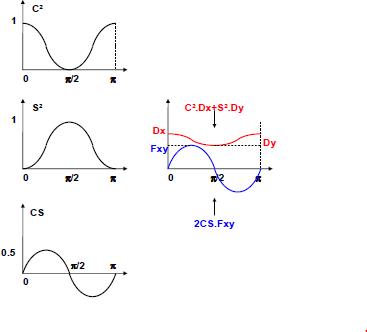
Il faut que la courbe rouge reste au-dessus de la courbe droite quel que soit l’angle q.

Pour trouver la solution optimale, qui minimise la quantité d’acier totale à mettre en place, c’est-à-dire Dx + Dy min, il faut satisfaire 2 conditions:

La relation (2) ci-dessus peut s’écrire :

f(q) = C² . Dx + S² . Dy – 2CS . Mxy = 0     (3)

ð       Dx + T² Dy – 2 T Mxy = 0 Avec T = tan (q)

La dérivée de la fonction f'(q) = 0 => f'(q) = 2S/C3 Dy – 2 C² Mxy = 0

=> Dy = Mxy/T (4)

On remplace Dy = Mxy /T dans (3) => Dx =T.Mxy

ð       Dx.Dy = Mxy.Mxy

Il est évident que q = 0 => Dx = 0 et pour q = p /2 => Dy = 0 Dx = Dy = Mxy est une solution de cette équation.

Conclusion

Avec la méthode Wood – Armer, les sections calculées dans une direction donnée par exemple (x,y) sont valables pour justifier la résistance quel que soit la facette d’orientation des sollicitations.

Wood – Armer simplifiée :

Wood – Armer générale :

Etape1 : Nous transformons les Mx, My et Mxy dans le système de coordonne a-b

Etape 2 : Nous calculons les moments de dimensionnement Wood-Armer

c. Méthode Capra Maury

Le principe consiste à considérer successivement différentes facettes de normale d’angle q.

Effort sollicitant sur une facette

Nous avons des efforts s’exerçant sur une facette quelconque d’angle q selon la théorie des plaques :

 
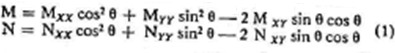
Les aciers peuvent être déterminés dans cette facette par un calcul de type : section rectangulaire soumise à de la flexion composée => on peut calculer Ainf(q) et/ou Asup(q).

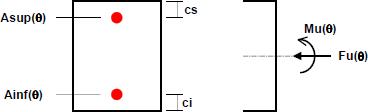
Effort résistant sur une facette

Nous avons :

Mise en équation

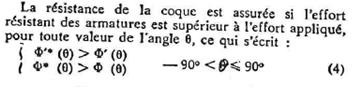
On doit déterminer Ax et Ay tels que :

C² . Ax + S² . Ay > A (q) quel que soit q et permettant par ailleurs de minimiser la somme Ax + Ay. Les logiciels tracent pour chaque pas de l’angle le domaine de validité d’inégalité ci-dessus :

 

On retient ensuite le point (Ax, Ay) permettant de minimiser la distance OQ en projection sur la première bissectrice (minimisation de Ax + Ay).

Conclusion

Contrairement à la méthode de Wood, la méthode Capra, est réalisable uniquement avec des logiciels (balayage des facettes) mais elle est plus adaptée pour des calculs en flexion composée. De même que la méthode de Wood, les sections calculées dans une direction donnée par exemple (x,y) sont valablent pour justifier la résistance quel que soit la facette d’orientation des sollicitations.

 

d. Méthode Baumann

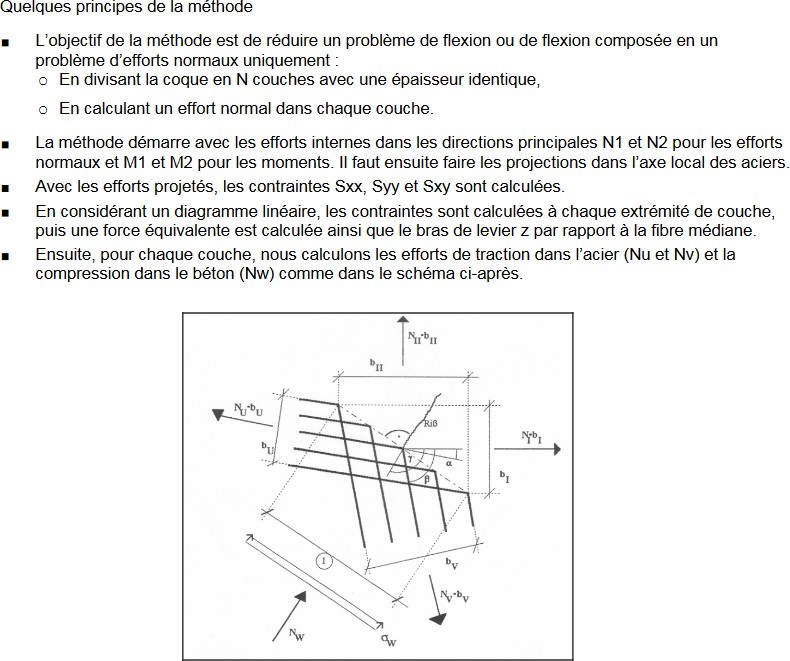
La méthode Baumann utilisée par (SCIA ou Advance Design) est également une méthode basée sur la recherche des sollicitations principales et la projection sur les directions données du ferraillage.

3. INFLUENCE DE L’ORIENTATION DU REPERE LOCAL SUR LES EFFORTS INTERNES ET LE FERRAILLAGE D’UNE PLAQUE

Nous analysons ci-après l’influence du changement de l’orientation du repère local sur une dalle modélisée avec ROBOT.

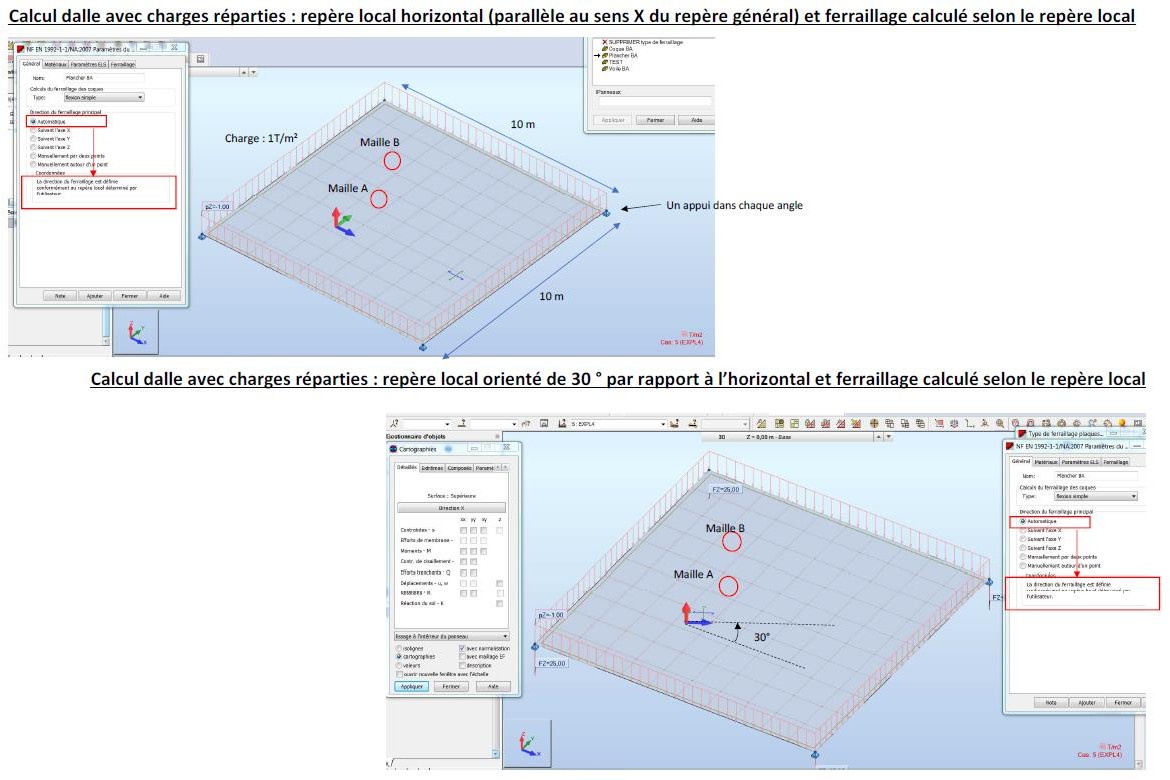
Pour chaque repère local diffèrent, les valeurs des moments Mxx, Myy, Mxy respectent bien la théorie des plaques the (voir 2.b.i)

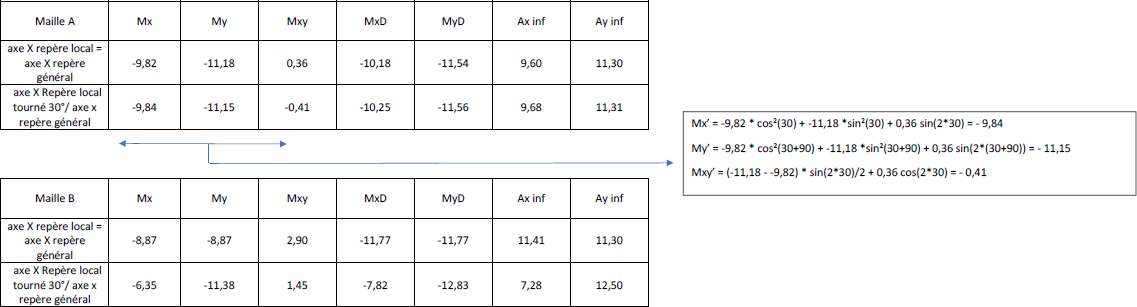
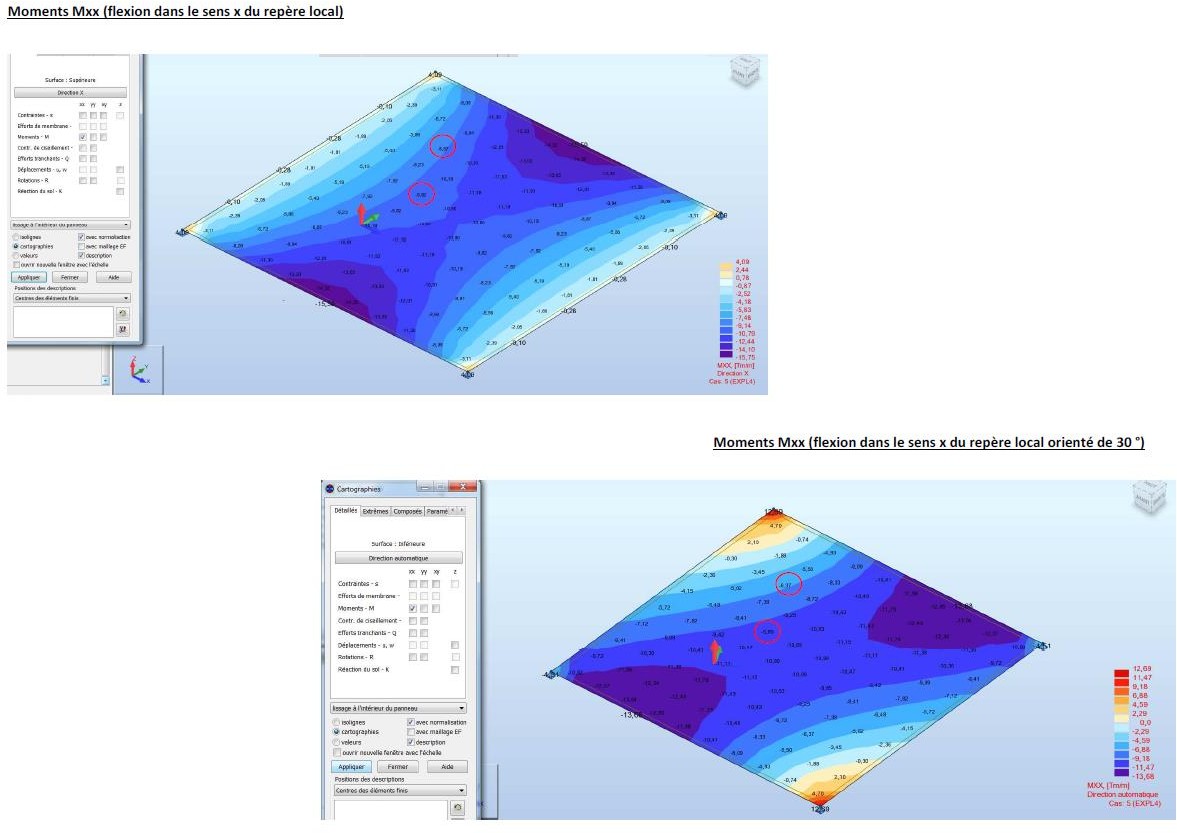
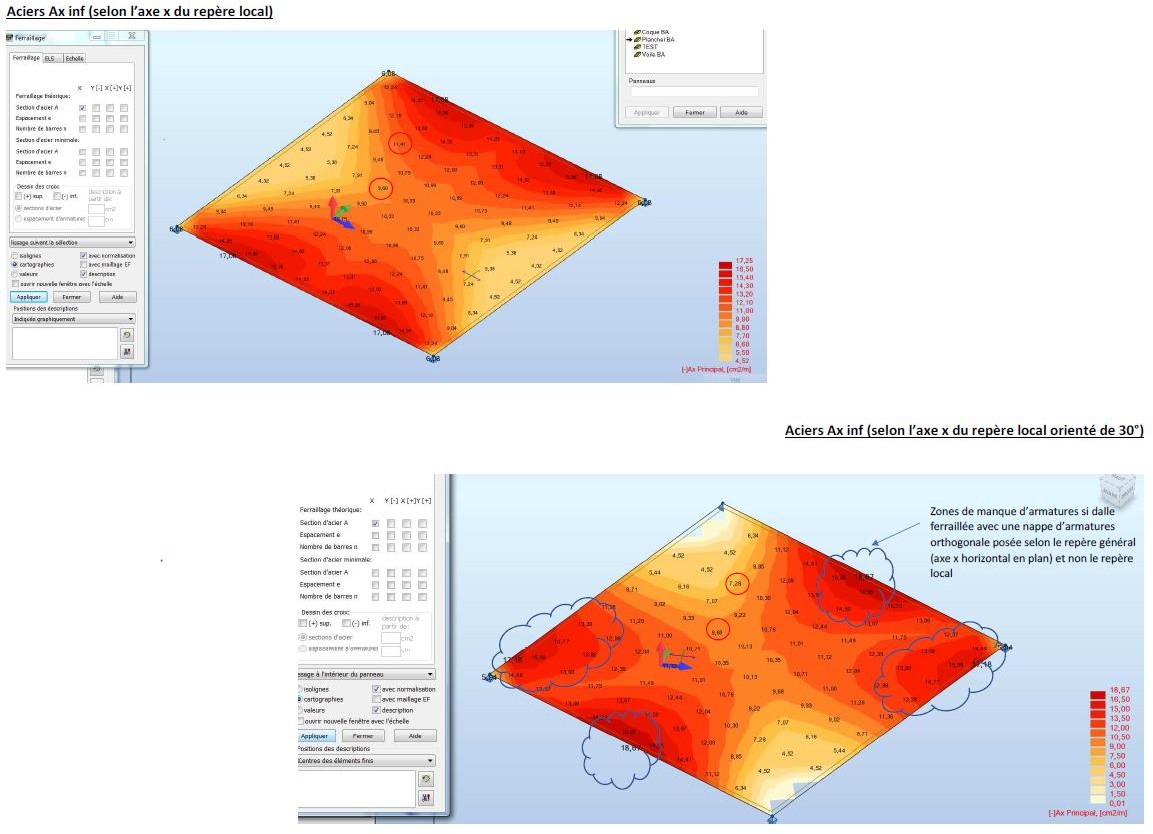
Nous obtenons des valeurs différentes du moment Wood – Armer pour chaque repère. Puis des sections nécessaires, calculées à partir de ces moments, différentes pour chaque repère local.

Or, le principe fondamental de la méthode Wood ou méthode Capra est que pour une orientation choisie, le ferraillage calculé est valable quel que soit l’orientation de la facette (Mxx, Myy, Mxy). De plus l’état des contraintes est forcément unique dans la plaque. Pour expliquer ce phénomène, nous étudions un modèle test très simple suivant 2 cas différents.

Cas 1 : Repère local dito le repère global

Cas 2 : Repère local orienté 30° par rapport par rapport à l’horizontal

 

a. Cas 1 : Repère local dito repère global

Mxx (Moment orienté suivant l’axe x) (T.m/ml) :

 

Myy (Moment orienté suivant l’axe y) (T.m/ml)

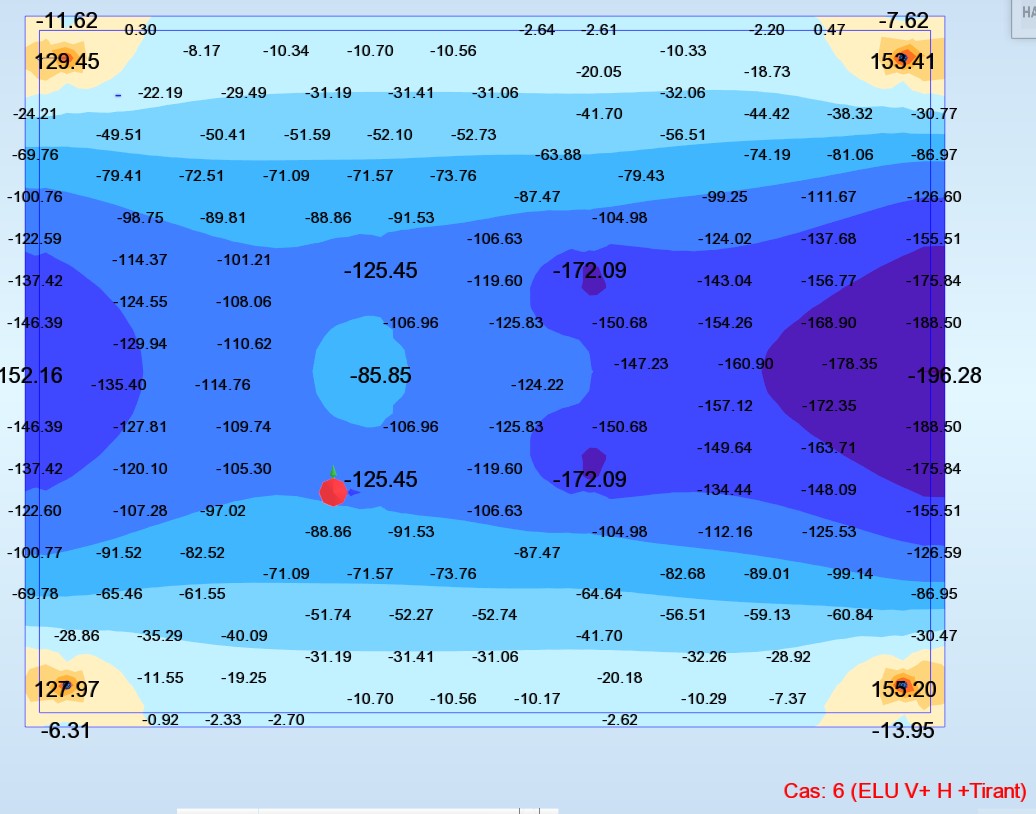
Mxy(Moment flexion-torsion) (T.m/ml)

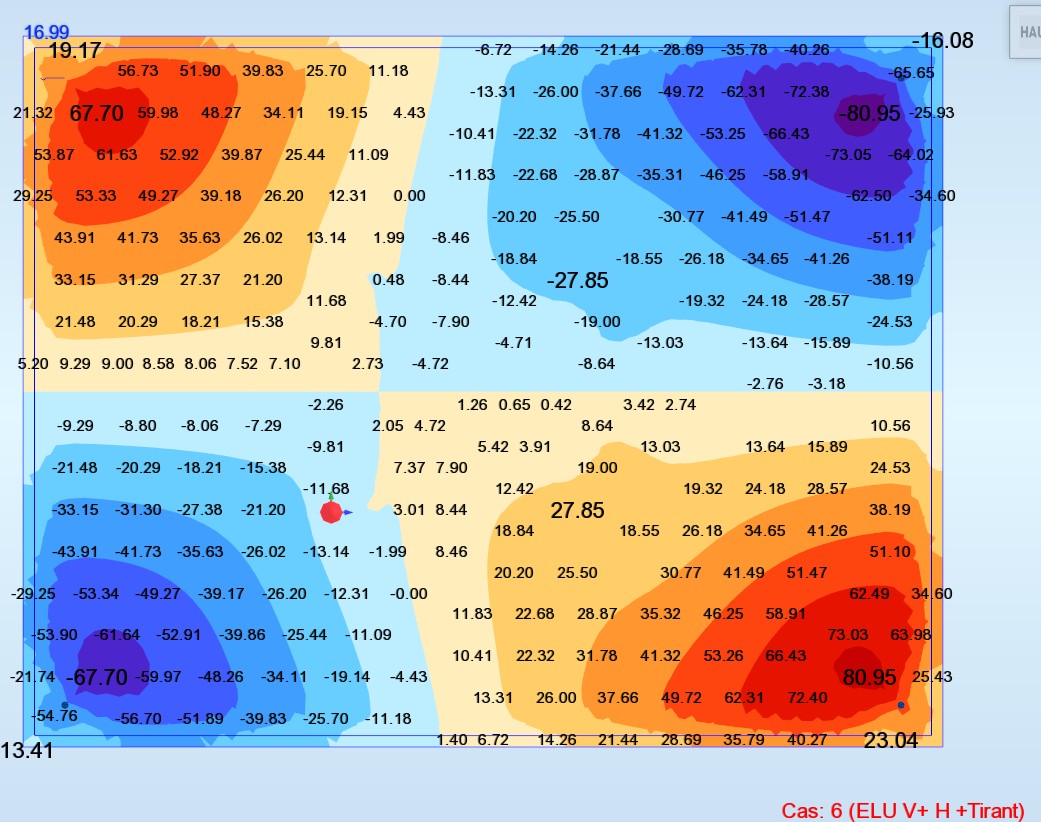
Mx Wood (Moment orienté suivant l’axe x) (T.m/ml)

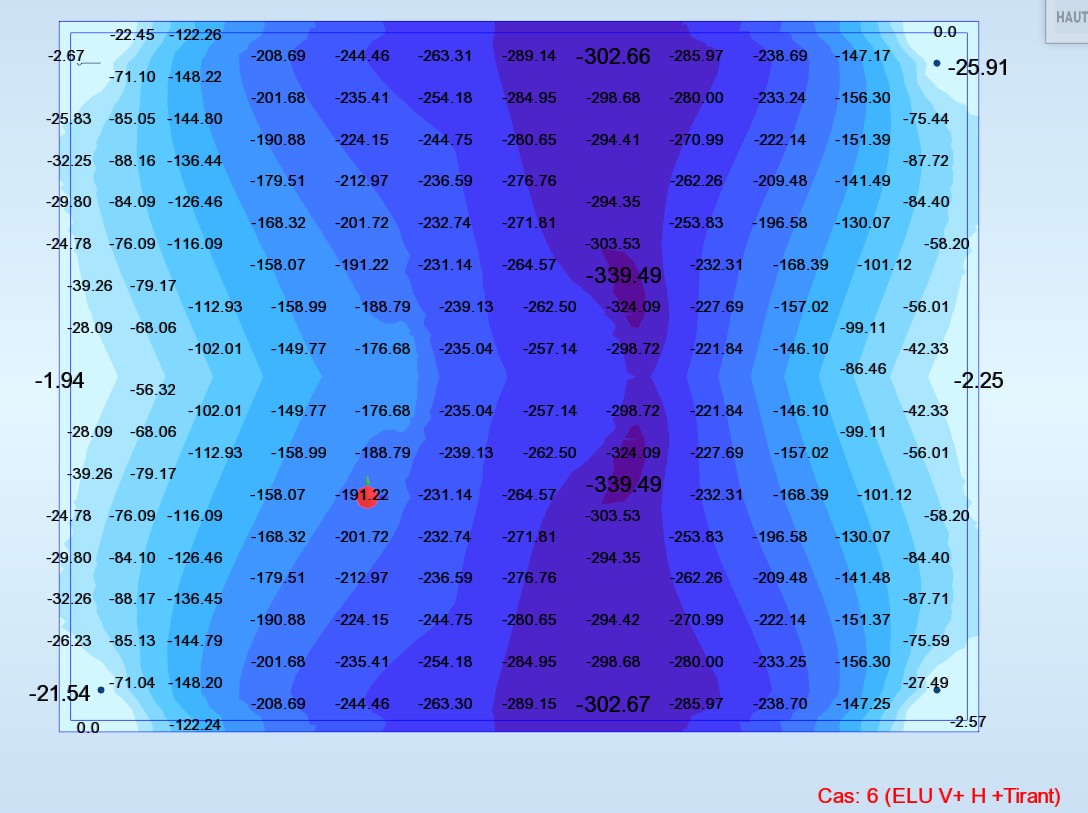
My Wood (Moment orienté suivant l’axe y) (T.m/ml)

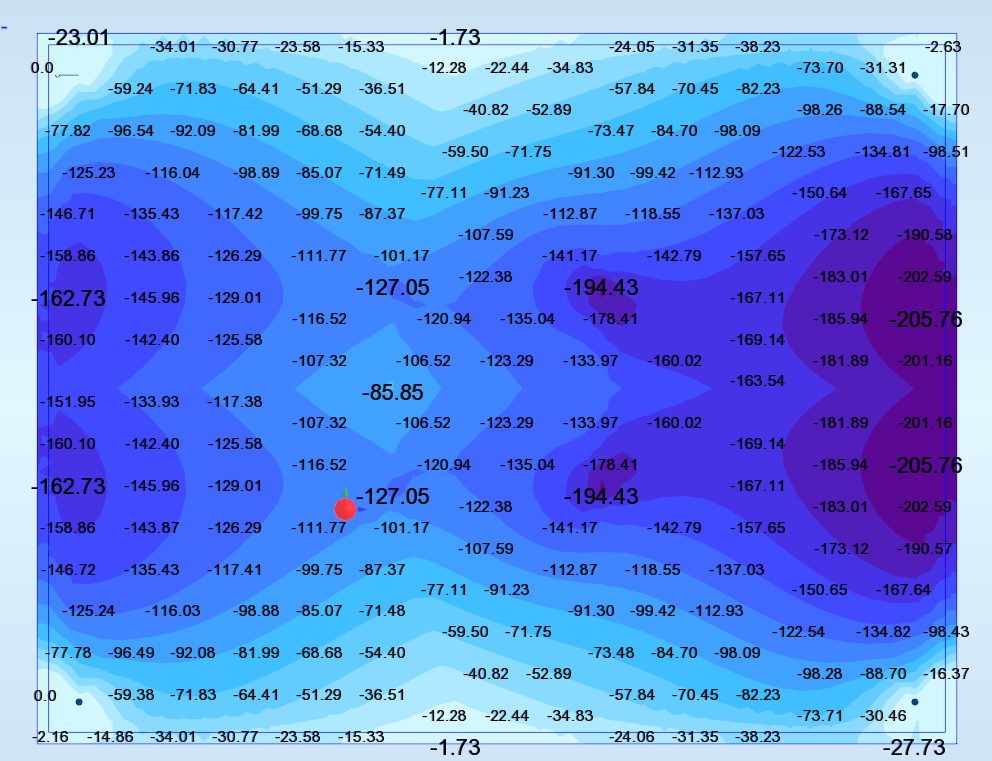
Ax inf (capra) (cm2/ml) :

Ax inf (cm2/ml) (wood):

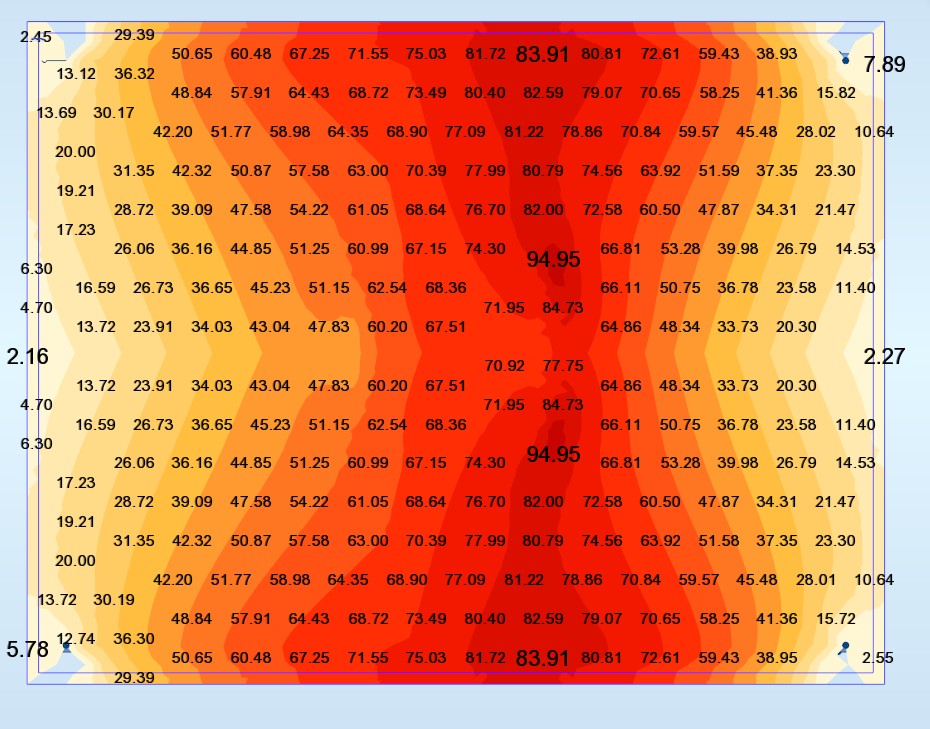
Ay inf (cm2/ml) (capra)

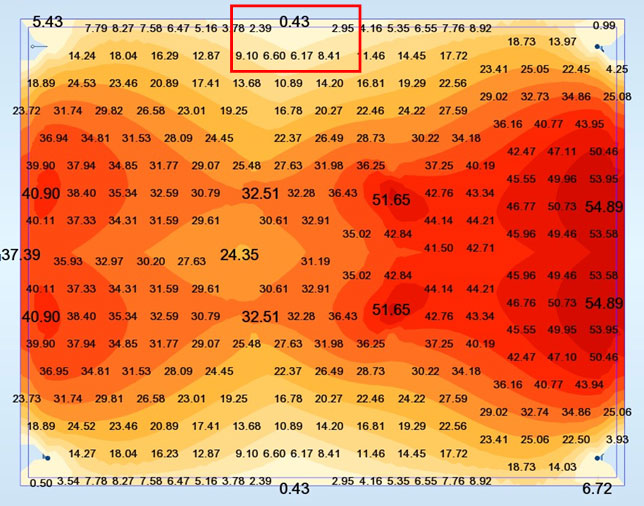
Ay inf (cm2/ml) (Wood)

Nous constatons qu’au bord de la dalle les moments Myy est Mxy sont presque nuls, par conséquence le moment Wood Armer (Mxx + Mxy) dans la direction x est presque égale à Mxx. La direction principale du moment est dans la direction Mxx (Mxy =0).

Pour les sections d’aciers, les 2 méthodes Capra et Wood donnent les résultats assez proches.

Logiquement, nous avons Ay proche de 0 et Ax = 80 cm2/ml

b. Cas 2 : Repère local orienté 30° par rapport par rapport à l’horizontal

Mxx (Moment orienté suivant l’axe x) (T.m/ml) :

 

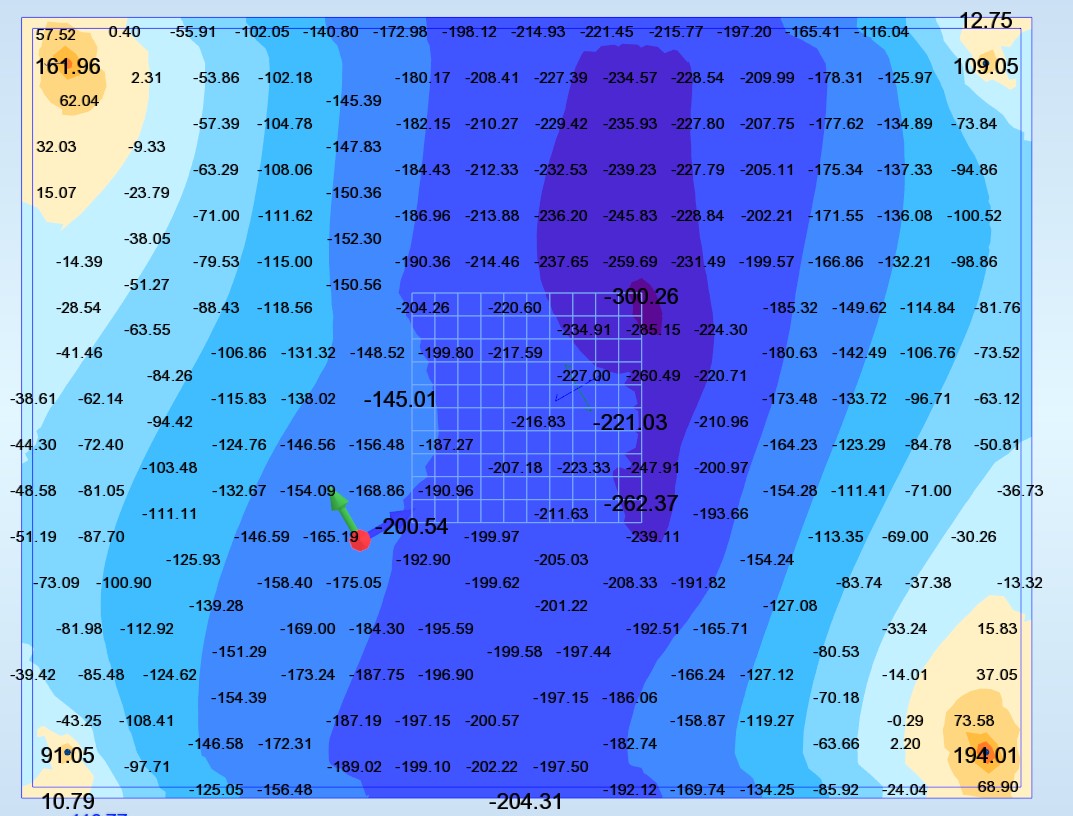
Myy (Moment orienté suivant l’axe y) (T.m/ml)

Mxy (Moment flexion-torsion) (T.m/ml)

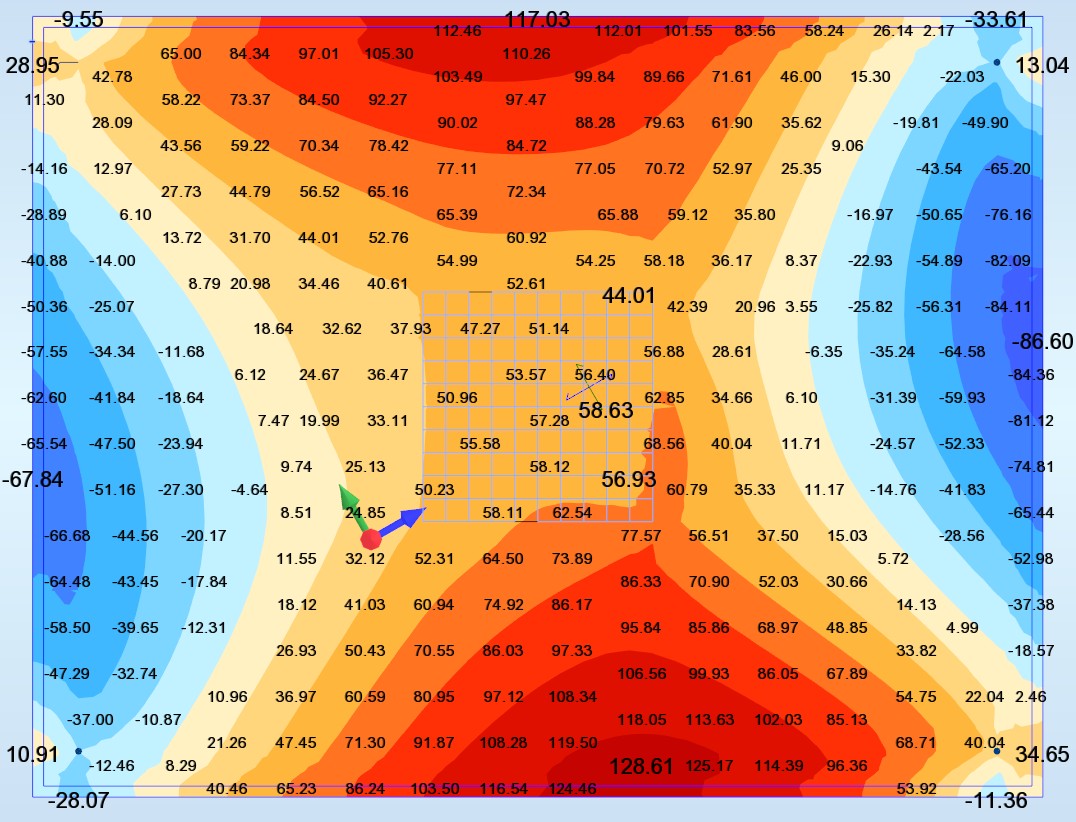
Mx Wood (Moment orienté suivant l’axe x) (T.m/ml)

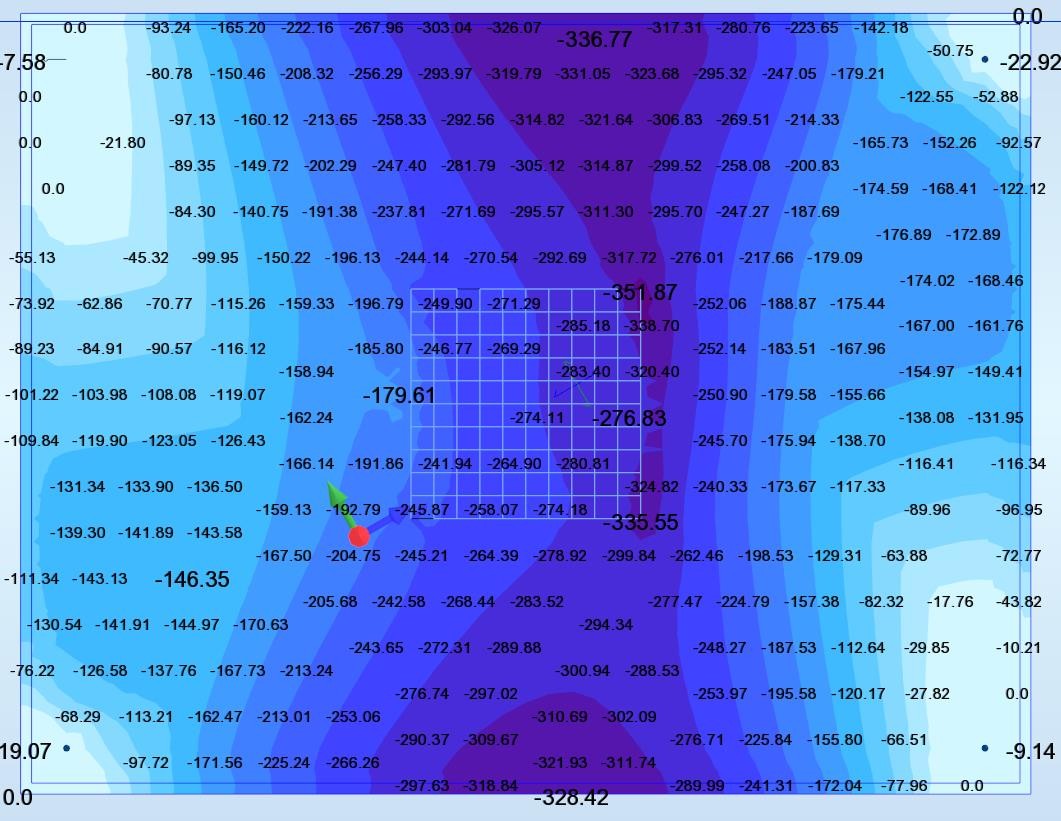
 My Wood (Moment orienté l’axe y) (T.m/ml)

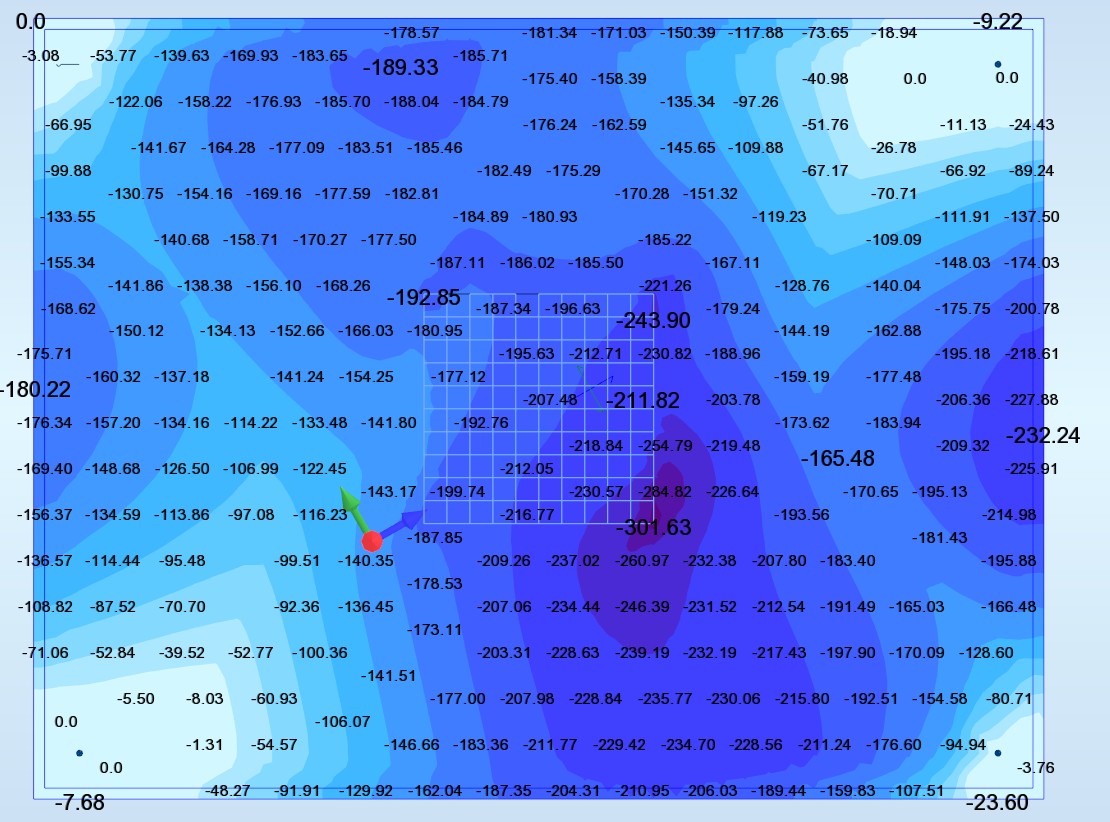
Ax inf (cm2/ml) (wood):

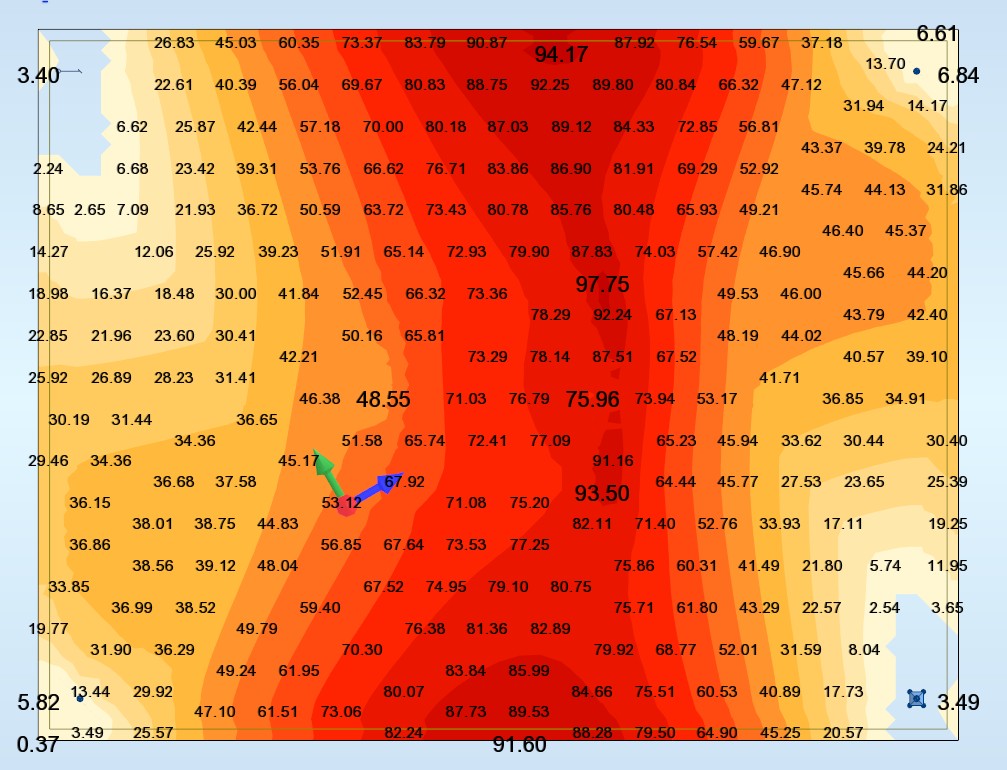
Ay inf (cm2/ml) (Wood)

Pour la maille au milieu du bord sup de la dalle, nous avons :

	Mxx (T/ml)	Myy (T/ml)	Mxy (T/ml)	MxD (T/ml)	MyD (T/ml)	Axi (cm2/ml)	Ayi (cm2/ml)
Cas 1	277	2	6	283	8	79	1
Cas 2	214	66	116	330	182	92	48

 

Nous constatons que pour le cas 2, nous avons des sections d’aciers très importantes suivant les 2 axes locaux si on arme la dalle suivant ces axes.

L’explication pour ce phénomène est que notre méthode de calcul, qui ne considère que les efforts normaux aux facettes et non les efforts tangents, n’est correcte que parce qu’elle considère successivement toutes les directions de facettes possibles, donc en particulier celle correspondant au repère principal (MXY=0).

Visiblement la direction principale la plus défavorable dans notre cas est l’axe x. Il faut C².Rx+S².Ry > C².

Mx+S².My + 2CS.Mxy quel que soit l’angle q.

Dans le cas 2, si on fait une projection R(q)= R(α) cos (q -α)² sur l’axe x : R(q)= 92*cos² (-30) + 48*sin ² (-30) = 80 cm2/ml >= 79 cm2/ml.

Ce résultant démontre que nous satisfaisons toujours l’équation C².Rx+S².Ry > C². Mx+S².My + 2CS.Mxy. Mais si la direction principale de renforcement est mal choisie, cela peut conduire à des sections par excès très importantes.

En réalité, la section strictement nécessaire suivant l’axe local orienté 30° par rapport à l’horizontal est : 79* cos² (30) = 59 cm2/ml suivant x et 79* sin² (30) = 20 cm2/ml suivant l’axe x.

Mais le logiciel cherche les sections pour que la projection sur l’axe principal soit supérieure aux sections calculées dans cet axe d’où les sections trouvées de 92 cm2/ml en x et 45cm2/ml en y.

c. Conclusion

Le choix de la direction principale de renforcement est crucial. Il est idéal de choisir cette direction proche de la direction principale du moment.

Il est conseillé d’armer les dalles avec une même orientation de ferraillages que les axes locaux pris en compte dans le calcul EF. Si dans certains cas liés par exemple à des sujétions de réalisation, il apparaît nécessaire de ferrailler avec une orientation spécifique et différente de celle prise en compte pour le calcul EF, nous devons faire une projection des ferraillages sur les directions locales prises en compte dans le calcul EF et s’assurer que les sections projetées sont supérieures aux sections calculées par le logiciel EF.